生成AIの活用 5 <誤差逆伝播法>
『高校数学でわかるディープラーニングのしくみ』の著書を読んで、ニューラルネットワークのしくみを理解するために、(その3)、(その4)と具体例で実際に表計算ソフトのエクセルで「学習」作業を行ってきました。
目的関数を最小にするパラメータ(重みと閾値)の決定には、実際に計算しなければ、雲をつかむような話で終わってしまうかも知れません。
ニューラルネットワークの「学習」を支える計算法が誤差逆伝播法です。
これまでの作業での私の体感では、この計算方法のしくみについてはブラックボックスでした。
著書では、計算方法のしくみの理解のために、最適化計算の基本となる勾配降下法の説明があります。
“勾配が最も急な所を選んで坂道を下る方法”ということを図とイラストで詳しい説明がなされていますが、誤差逆伝播法も勾配降下法が基礎になっています。
勾配降下法の説明の中に、この著書名にもなっている“高校数学でわかる”という微分やベクトルの数式がたくさん出てきます。
以下にベクトルの内積の公式が出てきます。
ベクトルa、bの大きさが一定のとき、その内積が最小になるのは
b=ーηa(ηは正の定数)
のときである。
勾配降下法の基本式は以下の公式です。
次の関数を満たすようにxをΔxだけ、yをΔyだけ少し変化させると、関数f(x,y)は最も減少する。
(Δx、Δy)=-η(∂f(x,y)/∂x、∂f(x,y)/∂y) (ηは正の小さな定数)
ここで、正の小さな定数η(イータ)はステップサイズ、ステップ幅などと呼ばれます。機械学習の分野では学習率とも言われます。
誤差逆伝播法はバックプロパゲーション法、略してBP法とも呼ばれます。
生成AI(その3)で調べた以下の課題を利用して、著書ではそのしくみを説明しています。
【課題Ⅰ】
5 x 4画素の白黒2値画像として読み取った手書きのアルファベット文字「A」「P」「L」「E」を識別するニューラルネットワークを作成しましょう。ただし、正解ラベル付きの128枚の文字画像(著書の末尾の付録に記載)を訓練データとします。活性化関数はシグモイド関数を利用します。
目的関数Eにおいて、重みwと閾値θ(合計79個)を順に微小に変化させたとき、関数Eが最も減少するのは次の関係が成立する場合である。ηは正の小さな定数とする。
(ΔwH11,…,ΔθH1,…,ΔwO11,…,ΔθO1,…)
=ーη(∂E/∂wH11,…,∂E/∂θH1,…,∂E/∂wO11,…,∂E/∂θO1)
※Hは隠れ層(中間層)、Oは出力層の表記
上記の右辺にある以下の微分式は「勾配」と呼ばれるベクトルである。
∂E/∂wH11,…,∂E/∂θH1,…,∂E/∂wO11,…,∂E/∂θO1
課題の入力が5 x 4画素の白黒2値画像で、79個もある勾配の要素1つひとつの微分計算をするという大変な作業になります。
そこで登場するのが、「誤差逆伝播法」です。
ここからが、「誤差逆伝播法」のしくみについてです。
平方誤差eを以下のように定義して、その計算に、ユニットの誤差(errors)と呼ばれる変数δ(デルタ)を導入し、以下のように定義されます。
e=1/2{(t1 – z1)^2 + (t2 – z2)^2 + (t3 – z3)^2 + (t4 – z4)^2}
※tは正解変数(正解が「1」)、zは出力層の出力
δHj=∂e/∂sHj (j=1,2,3)
δOk=∂e/∂sOk (k=1,2,)
※sHは隠れ層(中間層)のユニットの入力の線形和
※sOは出力層のユニットの入力の線形和
「ユニットの誤差」δで、平方誤差eの勾配成分を表すと以下のように簡単になります。
∂e/∂wHji=δHjxi、∂e/∂θHj=ーδHj
(i=1,2,…,12、j=1,2,3) ※xは入力層にあるユニットの出力を表す変数名
∂e/∂wOji=δOjhi、∂e/∂θOj=ーδOj
(i=1,2,3、j=1,2) ※hは隠れ層(中間層)にあるユニットの出力を表す変数名
この式の証明には偏微分の知識が要求されます。
恐らく、この著書の読者の大半はここで理解の壁にぶち当たり、この先を読破するのを諦めるのではなかろうかと思いました。実は私もその一人ですから。
諦めかけていたら、巻末の付録に証明が載っていました。高校の教科書では「合成関数の微分」と呼ばれる定理を利用して、偏微分のチェーンルールから説明がされていて、遠い昔の記憶が蘇ってきました。
突然、話は変わりますが、私が大学生だったころに、就職難に備えて高校理科の教員免許を取得するために、母校での教育実習に行った時のことを思い出しました。実習期間は短期間の集中実習ということで科目は数学でした。その頃は教材プリントを自前で作って配るプロセスの機材は、謄写版(ガリ版)でした。ちょうど難しい対数のところで、手書きのグラフや数式を藁半紙(わらばんし)に刷って配りました。自分の拙い教え方で生徒に理解してもらえたのか心配でした。帰りがけに古びた校舎の2階窓から数人の女生徒が“先生”と言って手を振ってくれたことを今でも鮮明に覚えています。教え方はどうあれ、母校の生徒たちは私を“先生”、“先輩”として迎い入れてくれたと、勝手な解釈ですが、あの時はとっても嬉しかったです。きっと今だったらAIを活用して、もう少し上手に説明できたかな?
この著書の著者は神奈川県立高等学校の教員の経歴があり、母校で教育実習をしたのかな、、、と自分の過去を振り返りながら、遠い昔の記憶に没入してしまいました。
兎に角、著者のわかりやすくて丁寧な解説には敬意を表する次第です。
さて、話を戻しますが、出力層の活性化関数をシグモイド関数z=σ(s)とすると、チェーンルールという微分公式の計算から、以下の式が得られます。
δOk=∂e/∂sOk=(∂e/∂zk )*(∂zk /∂sOk)
=(∂e/∂zk)* σ’(sOk) (k=1,2,…,4)
∂e/∂zk=ー(tkーzk)
上記の下の式を上の式に代入して以下の式が得られます。
δOk=ー(tkーzk)σ’(sOk) (k=1,2,…,4)
上記同様に隠れ層(中間層)の「ユニットの誤差」δHjについても以下の式が得られます。
δHj=(δO1wO1j+・・・+δO4wO4j)σ’(sHj)
(j=1,2,…,4)
ニューラルネットワークの計算では、隠れ層(中間層)から出力層に向かいますが、「ユニットの誤差」δの算出は、逆に、出力層から隠れ層に向かいます。これが「誤差逆伝播法」と呼ばれる理由です。
ここまでで、何とか私も「誤差逆伝播法」のしくみについて著者の説明に追い付いてきたような気がします。式の右辺にシグモイド関数σの微分形σ’が含まれていますが、
σ’(s)=σ(s){1ーσ(s)}
の関係から、微分の項をなくすことができます。
最後に、「誤差逆伝播法」についてもExcelで体験してみることにしましょう。
Excelの「ソルバー」と呼ばれる最適化ツールに頼ることなく、ExcelのVBAと誤差逆伝播法を組み合わせて、自前で重みと閾値を決定しましょう。
計算方法のしくみについてはブラックボックスでしたが、今回はExcelのVBAでの誤差逆伝播法プログラムを著書中の記述(一部コメントが勾配降下法になっていましたので誤差逆伝播法に修正)を以下に記します。
Sub Macro1()
Sheets(“BP”).Select
‘初期値を現パラメーターにコピー
Range(“C91:G110”).Select
Selection.Copy
Range(“C15:G34”).Select
Selection.PasteSpecial Paste:=xlPasteValues
‘誤差逆伝播法
For GradientDescent = 1 To Range(“C5”)
Range(“D5”) = GradientDescent
‘勾配の更新
Range(“C61:G80”).Select
Selection.Copy
Range(“C15:G34”).Select
Selection.PasteSpecial Paste:=xlPasteValues
Next GradientDescent
End Sub
上記のプログラムは勾配降下法を3変数以上に拡張した関数fが最も減少するするときの以下の関係式を計算しています。
(Δx1,Δx2,…,Δxn)=ーη(∂f/∂x1,∂f/∂x2,…,∂f/∂xn)
※上式に従い、点(x1,x2,…,xn)から点(x1+Δx1,x2+Δx2,…,xn+Δxn)へ移動させるときに
ステップサイズ:η および計算の繰り返し回数の設定値をVBAプログラムでは使用しています。
‘初期値を現パラメーターにコピー
「C91:G110 の値(初期値0)を C15:G34 に値のみコピーして上書きしている」
‘誤差逆伝播法
計算の繰り返し回数は「C5」で 500回
ステップサイズηは「C8」で 0.05
「C61:G80 の値を C15:G34 に値のみコピーして上書きしている」
驚くほどに単純な処理でソルバーに代わるVBAプログラムの威力に感動しました。どうしてセルのコピペでだけで「誤差逆伝播法」の計算ができるのかは、埋め込んだ関数がどこを参照しているかで理解することができました。
「C61:G80」の中に埋め込んだ関数は「C15:G34」と「C38:G57」の値を参照した計算をしています。例えば先頭のC61では 「C61=C15-$C$8*C38」 のように 「更新値=前回値ーη*勾配」 という関数を実行したことになっています。
前出(その3)の【課題Ⅰ】でのニューラルネットワークの確認では、誤差逆伝播法は用いずに、簡単に重みと閾値のパラメーターの初期値を設定し、目的関数Eを最小化するためにソルバーを実行しました。
今回は、そこで使用したワークシートに追記する方法でユニットの誤差δを利用して勾配計算をしています。
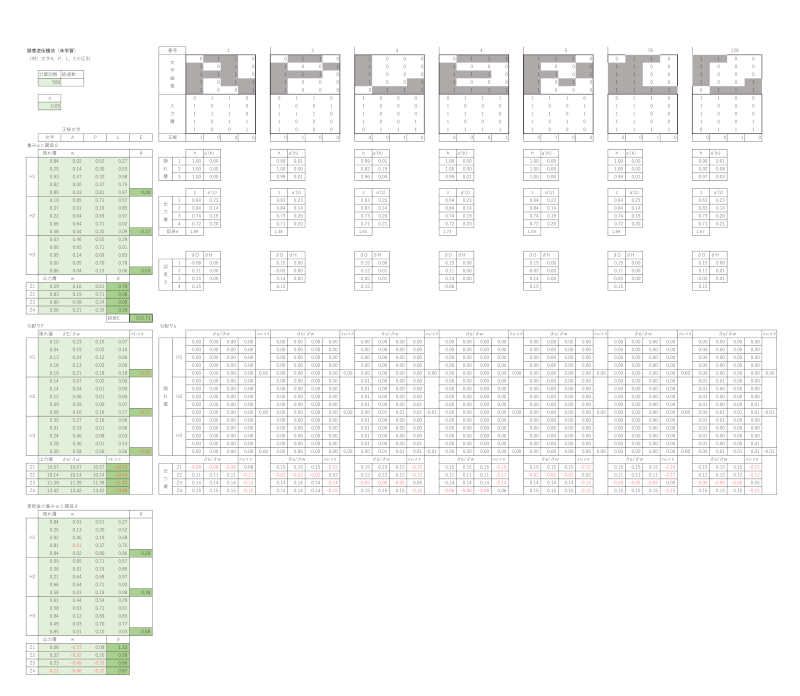
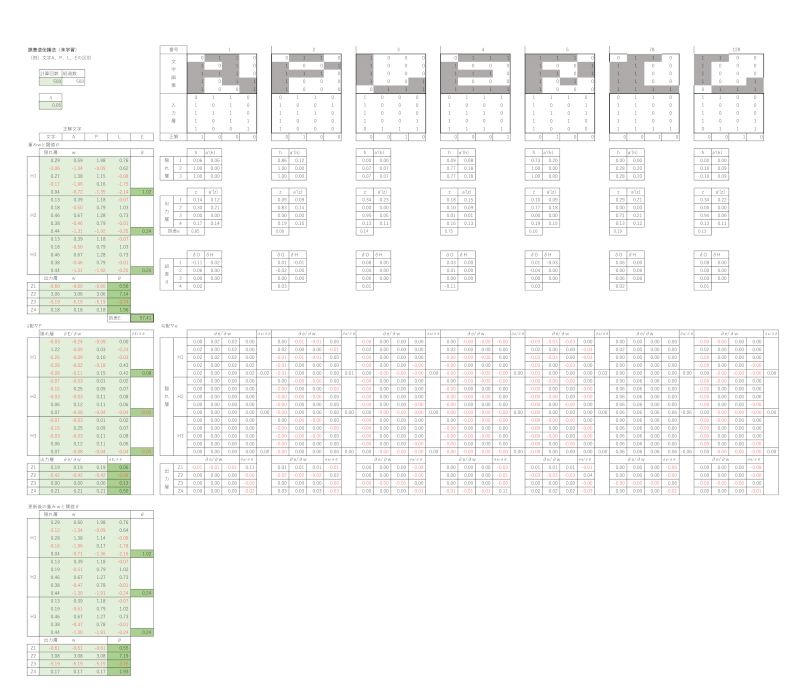
以下が未学習時と学習済みの結果です。画像では細かくて数値が読みづらいので感覚でお伝えします。
< 誤差逆伝播法(未学習)>
< 誤差逆伝播法(学習済み)>
計算回数: 500回
ステップサイズ η:0.05
生成AIの活用(その3)、(その4)、(その5)の3回に亘って、ニューラルネットワークの学習作業を表計算ソフトのエクセルで行うことによって、“AIはこのような考え方で判断を下しているのだ!”ということが実感できましたでしょうか?
私は、皆さんにアイデンティティとして語ることによって、そのことで理解が深まりました。
ここまで、ご一読いただき、ありがとうございました。




コメント