前回(その2)でChatGPTのお話をしましたが、生成AIの活用をする前に、AIの仕組みをしっかり理解しておこうと思い、市営の小諸図書館で書籍を探しました。
“AIはこのような考え方で判断を下しているのだ!”ということが実感できるとの触れ込みの以下の本を見つけました。
『高校数学でわかるディープラーニングのしくみ』(著者 涌井貞美)
ディープラーニングは人の脳神経細胞のネットワーク(ニューラルネットワーク)をモデル化したAIの実現方法ですが、従来の機械学習からコンピュータが“特徴抽出”という手法を用いて、特徴を自らつかんでいくというものです。
この著書では入力層・中間層・出力層の3層のうち、中間層を複数の層に分けることによる畳み込みニューラルネットワーク(CNN、Convolutional Neural Network)が昨今のAIブームを巻き起こした立役者であるとして、その仕組みをわかりやすく解説しています。
数式がたくさん出てくるのですが、“高校数学でわかる”と題しているように、高校時代の記憶を呼び起こすレベルで理解はできていると思っています。とは言っても、300頁ほどあるうちの3分の2ぐらいのところですが、私の不注意によるアクシデントがあり、読書は途中で中断しています。これはアクシデントではなく、ハプニングと見なしたいです。
ここで、生成AIのお話はひと休みとして、余談になりますが、そのハプニングのお話をします。
・~・~・~・~・~・~・~・~・
私が70歳で会社勤務を終えてからというものは、自宅に籠ってられず、市営の小諸図書館に通うようになりました。何故かといえば、手前勝手ですが、自宅では雑用が多くて自分の好きなことに集中できないのです。そこで、“亭主は達者で留守がいい”と言いますから、平日は会社通勤と同じように図書館にパソコンを持ち込んで、Wi-Fiを利用してこのブログを更新したり、図書館の蔵書を文献代わりに読書をするようになりました。自宅から車で20分ぐらいの範囲で小諸図書館の他に佐久市立中央図書館、御代田町立図書館、軽井沢町立図書館がありますので、休館日等には気まぐれにそちらの何処かに通います。図書館は私のような年配者から受験生など、人がいるのに静かで落ち着いた雰囲気です。とりわけ私は小諸図書館の雰囲気が好きです。公共のスペースだけど、他の場所とは全く違うプライベートな空間を許容してくれる気がします。
水分補給のため紅茶を入れた水筒を手提げ袋の中に入れて通うのですが、その日は手提げ袋に図書館で借りた本を一緒に入れて帰りました。この『高校数学でわかるディープラーニングのしくみ』という著書を家に帰って続きを読もうとしたら、なんと!水筒から漏れた紅茶で色が付いていました。
こんな時、どうしますか?
私はその時、返却しても差し支えがないように濡れた部分を拭き取り、修正しようと試みました。どうしても紅茶の色は残ってしまいます。次にこの本を借りる人は、きっと不快感を感じるだろうと思いながら、賠償方法を確認するため図書館に電話をしました。頻繁に図書館に通い出してからのことなので、電話の相手の担当者の顔を思い浮かべながら現状をお話しました。親切な応対で、やっと混乱から解放されたような気持ちになれました。早速、BOOKOFFのwebサイトで中古の本を探して注文しました。定価は税抜きで2,200円でしたが、中古で税込み900円で入手できました。担当者が親切に「中古でもいいですよ」と言ってくれたので、安価で済み、しかも紅茶で汚れた本は私の所有物となりました。
考えてみると、900円の投資で“AIの仕組みや高校数学の学び直し”の教材が手に入ったことになります。
これでやっと著書の続きを心置きなく読むことができるようなりました。私はこの本を人生を変えるような運命的な出会いだと思い、とっても大切にしています。
・~・~・~・~・~・~・~・~・
それでは、続きの著書『高校数学でわかるディープラーニングのしくみ』の内容を紹介します。
前述で今のAIブームの立役者である畳み込みニューラルネットワークのことを紹介しましたが、著書の中では、このネットワークの目的関数をニューラルネットワークから順に畳み込みの中間層のプーリング層まで図を交えてわかりやすく解説されています。
目的関数とは出力層の出力と正解との誤差を関数化したものです。
「学習」とはこの誤差の総和である目的関数を最小化することであります。
ここまで、文章のみでザックリ説明しましたが、きっとこの説明では理解していただくことは難しいと思います。この著書の特徴は図解説明ですから。
わかりやすいニューラルネットワークのレベルで「パラメータ」の説明をしておきます。
重み(W)は特徴抽出のための入力層と中間層との連結の強さを表します。
閾値( θ )は生物的にはニューロンの個性を表現する値で敏感度を表します。
入力(X1,X2,・・・,Xi)を考え、各入力に重み(W1,W2,・・・,Wi)を与え、閾値をθとすると、入力と出力の関係をテキストのみで以下に表記してみました。著書での図解説明とは別に私なりに作成しましたのでわかりづらいかも知れませんが、ご容赦ください。
【入力層X】
入力(X1,X2,・・・,Xi) ーーー→ 中間層へ
【中間層】
【隠れ層H】
重み(Wh1,Wh2,・・・,Whj)、 閾値 θh
ーーー→ H1,H2,・・・,Hj ーーー→ 出力層へ
【出力層Z】
重み(Wo1,Wo2,・・・,Wok)、 閾値 θo
ーーー→ 出力(Z1,Z2,・・・,Zk)
この関数は高校で教わりましたかね?
シグモイド関数とは
脳の神経細胞(ニューロン)の働きを数式で表現するときに、出力が0か1かの不連続関数であるステップ関数を活性化関数(伝達関数)としていましたが、微分しやすい活性化関数に置き換えたものがシグモイド関数です。
σ(x)= 1 /( 1 + EXP( – x ))
シグモイド関数をエクセル用に記述しましたが、ステップ関数に似ていて滑らかな曲線で普通に微分法が適用できます。
入力の線形和をs、出力をyとし、シグモイド関数σで表すと以下となります。
s = w1・x1 + w2・x2 + ・・・ + wn・xn – θ
y = σ(s)
ソルバーとは
Microsoft Excelをはじめとする表計算ソフトの機能の一種で、複数の変数を含む数式において、目標とする値を得るための、最適な変数の値を求めることができる機能のことです。 ソルバーでは、複数の変数の値を変化させながら変数の相互関係を判断し、最適な値を算出することができます。
この著書で感心したことは、冒頭でこの著書の触れ込みとして“AIはこのような考え方で判断を下しているのだ!”ということが実感できたことです。
具体的には普段お馴染みの表計算ソフトエクセルでソルバーを実行して目的関数の最小値を計算することによって、その「学習」結果の解釈を実感できたということです。
表計算ソフトはニューラルネットワークの計算と相性が良い性質を持っています。
上記のような数式で表される抽象化したニューロンをユニット(ノード)と呼びますが、1ユニットに1セルが対応できるからです。
著書ではニューラルネットワークの具体例として、以下の課題が与えられました。畳み込みニューラルネットワークでの課題の提示もありましたが複雑になるので、ここでは原理を理解することを優先し、畳み込みは割愛させていただきます。
【課題Ⅰ】
5 x 4画素の白黒2値画像として読み取った手書きのアルファベット文字「A」「P」「L」「E」を識別するニューラルネットワークを作成しましょう。ただし、正解ラベル付きの128枚の文字画像(著書の末尾の付録に記載)を訓練データとします。活性化関数はシグモイド関数を利用します。
【ソルバー実行】
① 目的関数は誤差Eの表記右のセルに以下の式を埋め込みます。
誤差E = 誤差e1+e2+e3+・・・+e128
ソルバーには目的関数の誤差Eとパラメータを設定し、最小値計算を指示します。
② 誤差eの表記右のセルに正解変数との平方誤差の計算式
③ 隠れ層のhのセルには隠れ層の出力計算式(シグモイド関数)
④ 出力層のzのセルには出力層の出力計算式(シグモイド関数)
以上の目的関数を含めて4種の計算式を埋め込んでソルバーを実行させます。
以下が結果です。
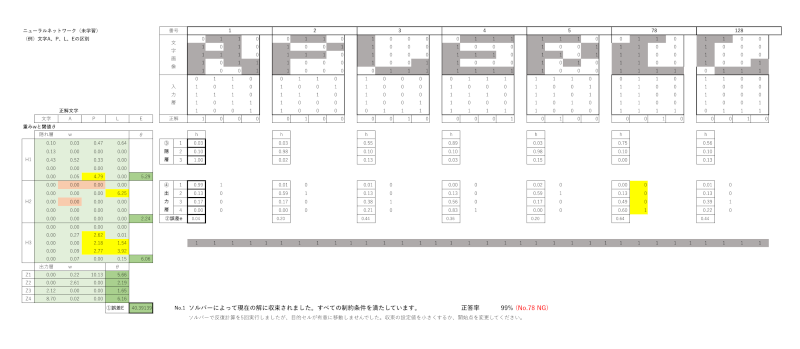
【1回目の結果】
【2回目の結果】
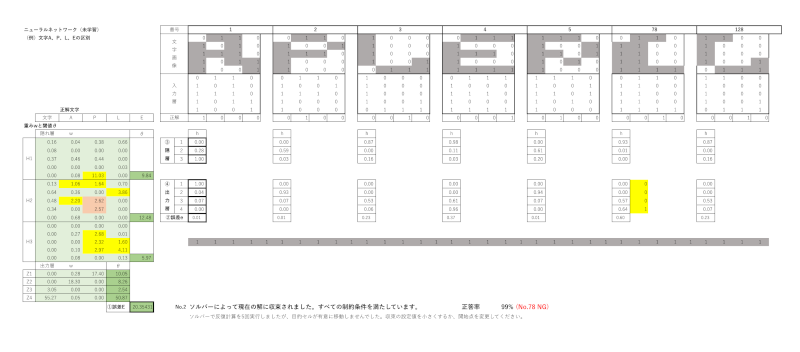
上記はエクセルのワークシートで、No.1~128のうち必要以外は非表示にして、作成したPDFファイルを画像形式のpngに変換した画像です。細かくて数値が読みづらいですが、感覚でお伝えします。1回目の隠れ層H1、H2、H3の初期値は著書の中で提示されたものを設定しました。ところが、試しでソルバーを実行してしまい、再設定しなかったので著書の初期設定値とは変わっています。
1回目、2回目の①誤差Eの目的関数Eの値は
E = 40.39(1回目)、20.35(2回目)
重みと閾値に対して、正解ラベルを正しく予測した率(正解率)は2回とも99%でした。
78番目のサンプル(訓練データ)が2回とも正解が「L」のところ「E」でした。
目的関数Eの数値の意味するところは、値として0~1を取りうる画素数5×4=20個の画像が128枚あるので著書での結果(E=25.41、正解率98%)はかなり良い値と考えられるとしていました。
以上のように、この著書によって、エクセルという身近なツールを使って、人の脳神経細胞のネットワークをモデル化したAIを体感できたことに感謝します。
まだ、この著書の完読までには時間がかかるかと思いますが、ここまでで哲学的な観点で一番言いたいことは、最初に種を蒔いておいたもの(初期の設定値)が学習をすることによって成長していく(正解を探していく)ことを実感したわけです。種には“世界に一つだけの花”になるための要素(重みや閾値)があって、形、色、匂いという唯一のもの(個性)を創り出しているということです。
これらは自然が創り出す技であり、あまりにも出来過ぎていることから、私には神様が創ったものとしか思えません。しかしながら、真理は哲学的な観点からだけではなく、科学的な観点から客観的な事実や法則として捉えていきたいと思っています。
次回からは少し具体的に、生成AIを活用したプログラミングについて投稿していきますので、よろしくお願いします。
追伸:
この“68歳の夢ブログ”の中で会社をつくるための資金稼ぎに、副業としてアフィリエイトを始めることにしました。ということは、私もアフィリエイターの仲間入りです。
記念すべき第一弾のアフィリエイト広告として、日本の停滞している経済の起爆剤となる成長へのライフシフトを促す人材養成講座を掲載しましたが、オープン案件からクローズド案件に移行したため、現在は申請中となっています。
今後は、第2弾、第3弾と投稿記事にできるだけ合致したようなアフィリエイト広告を掲載して行く予定ですので、何卒よろしくお願いします。




コメント