前回(その3)で生成AIがどんな仕組みで判断を下しているのか、著書『高校数学でわかるディープラーニングのしくみ』を読んで感動したことをお伝えしました。その時はこの著書の3分の2(200頁)ぐらいまでのところでしたが、その後、残り3分の1を完読し、もやもやしていた部分がすっきりしました。
そこで、前回では生成AIを活用したプログラミングについて投稿するとお伝えしましたが、上記のもやもやした部分をここではもう少し掘り下げていきます。
■ 畳み込みニューラルネットワーク(CNN)のしくみ
前回では、著書の4章でニューラルネットワークのしくみが見えてきたことはお話しましたが、5章の畳み込みニューラルネットワーク(CNN)については、より複雑になるので説明を割愛させていただきました。AIブームを巻き起こした立役者であるにもかかわらず、お伝えする私もまだ学びの途中です。
畳み込みニューラルネットワークのしくみについても、基本的にはニューラルネットワークと同じように、目的関数を最小にするフィルター、重み、閾値のパラメーターをソルバー実行によって実際に求めてみます。著書の中での与えられた課題で実際に求めてみて、AIの「学習」を体感することに意味があります。
基本構成は単純なニューラルネットワークと同様、入力層、隠れ層、出力層の3層です。隠れ層では入力層のユニットを小分けにして調べる畳み込み層と更に圧縮して調べるプーリング層があります。
著書の中で畳み込みニューラルネットワークについても以下の具体的な課題が提示されました。
【課題Ⅱ】
9×9=81画素のモノクロ画像として読み取った手書き数字「1」、「2」、「3」、「4」を識別する畳み込みニューラルネットワークを作成しましょう。ただし、正解ラベル付きの192枚の数字画像を訓練データとします。活性化関数はシグモイド関数を利用します。
ここで用いる手書き数字の「1」~「4」はNIST(National Institute of Standards and Technology、米国国立標準技術研究所)のMNISTと呼ばれる手書き数字の画像データセットで著書の末尾の付録にピックアップした192個の全データが掲載されています。
【ソルバー実行】
① 目的関数は誤差Eの表記右のセルに以下の式を埋め込みます。
誤差E = 誤差e1+e2+e3+・・・+e192
ソルバーには目的関数の誤差Eとパラメータを設定し、最小値計算を指示します。
ここから先が畳み込みニューラルネットワークの隠れ層における畳み込み層のフィルターの重みと閾値、プーリング層のプーリングテーブルをどのように設定したらよいのかがよくわかりませんでした。ですから、単純なニューラルネットワークの時のような以下の②以降は手探り状態となりました。
② 誤差eの表記右のセルに正解変数との平方誤差の計算式
③ 隠れ層のhのセルには隠れ層の出力計算式(シグモイド関数)
④ 出力層のzのセルには出力層の出力計算式(シグモイド関数)
上記のニューラルネットワーク時の3項目は、番号1/192、畳み込み層フィルター1/3、ブロック1/36のエクセルのセル(L12)に以下の式が埋め込まれていることをヒントにソルバーに引き渡すための設定を確認しました。
L12 = 1/(1+EXP(-SUMPRODUCT($E$12:$H$15,L2:O5)+$E$24))
このSUMPRODUCTというExcelの関数ですが、指定された複数の配列の対応する要素同士を掛け合わせた後、それらの積の合計を計算する関数です。
=SUMPRODUCT(A1:A3, B1:B3) は、A1*B1 + A2*B2 + A3*B3 の計算結果を返します。
ここでやっと、埋め込まれた関数をヒントに手探り状態から脱することができました。
しかしながら、正解ラベル付きの192枚の数字画像を訓練データとし入力層のセルに登録し、畳み込み層、プーリング層、出力層それぞれのセルに上記のような関数を埋め込んでいく作業はとても大変です。私はソルバー実行の準備段階で音を上げてしまい、結果を体感できませんでした。
著書での結果ですが、正解率は88%でした。仮定した畳み込みニューラルネットワークでは、フィルターを3枚しか用意していなかったので、それを思えば、まずまずというところだとの著者の考察に私も納得しました。
前回(その3)、今回(その4)を通して、ここまでが、単純なニューラルネットワークと畳み込みニューラルネットワーク(CNN)のしくみですが、このニューラルネットワークに少し修正を加え、記憶機能を持たせたしくみがリカレントニューラルネットワーク(RNN)です。そこで今回は以下にRNNについてもお話したいと思います。
■ リカレントニューラルネットワーク(RNN)のしくみ
人の会話やモノの動きのような前後関係に意味のある時系列データを扱えるモデルです。
前の入力の処理結果(出力)を再度入力に取り入れるという回帰するユニット(コンテキストノード)を隠れ層に状態層として加えることによって機能しています。まずは具体例として、スマートフォンに言葉を入力する際、前の文字を入れると次の文字が予測されて表示されるしくみを以下の課題として調べていきます。
【課題Ⅲ】
次の表にある言葉を「ひらがな」で入力する際、「読み」の最後日の文字が、その手前までに入力された文字から予測されるリカレントニューラルネットワークをつくりましょう。
| 言葉(読み) | 入力文字 | 最後尾の文字 |
|---|---|---|
| 伊予市(いよし) | 「いよ」 | し |
| 意志よ(いしよ) | 「いし」 | よ |
| 良い詩(よいし) | 「よい」 | し |
| 吉井(よしい(人の名)) | 「よし」 | い |
| 恣意よ(しいよ) | 「しい」 | よ |
| 詩良い(しよい) | 「しよ」 | い |
| 詩よ(しよ) | 「し」 | よ |
| 葦(よし(植物名)) | 「よ」 | し |
リカレントニューラルネットワークの今回の課題に沿って言葉の長さを最大3文字としたテキストのみでの展開図を作成しました。著書の展開図を私なりにテキストのみで勝手に表記してみましたのでご容赦ください。
【入力層X】
X1,X2,X3 ーーー→ 中間層へ
【中間層】
【隠れ層H】【状態層C】
ーーー→ C1→H1,C2→H2 ーーー→ 出力層へ
【出力層Z】
ーーー→ Z1,Z2,Z3
畳み込みニューラルネットワークの説明時に小分けした区域のことをブロックと呼ぶことにしていますが、同様に以下のようにブロック1での1文字目の処理結果がブロック2の2文字目に結合されるしくみを著書ではわかりやすい展開図によって説明しています。ここでは著書の展開図を私なりにテキストのみで勝手に表記してみましたのでご容赦ください。
【ブロック1】
【入力層1】 【隠れ層1】
X1,X2,X3 → H1,H2 ーーー→ ブロック2へ
【ブロック2】
【状態層C】【入力層2】 【隠れ層2】
ーーー→ C1,C2 X1,X2,X3 → H1,H2 ーーー→ 出力層へ
【出力層】
ーーー→ Z1,Z2,Z3
テキストのみでの説明では、かえってわかりづらくしてしまったかも知れません。
【ソルバー実行】
① 目的関数は目的関数Eの表記右のセルに以下の式を埋め込みます。
誤差E = 誤差e1+e2+e3+・・・+e8
ソルバーには目的関数の誤差Eとパラメータを設定し、最小値計算を指示します。
② 誤差eの表記下のセルに以下の正解変数との平方誤差の計算式を埋め込みます。
平方誤差e = (t1 – z1)^2 + (t2 – z2)^2 + (t3 – z3)^2
③ ブロック1の隠れ層のhのセルには隠れ層の出力計算式(シグモイド関数)を埋め込みます。
④ ブロック2の状態層のcのセルには以下のブロック1との関係式を埋め込みます。
c1[2]= h1[1]、c2[2]= h2[1]
⑤ ブロック2の隠れ層のhのセルには出力層への出力計算式(シグモイド関数)を埋め込みます。
⑥ 出力層のzのセルには出力層の出力計算式(シグモイド関数)を埋め込みます。
以上の目的関数を含めて4種の計算式を埋め込んでソルバーを実行させます。
以下が結果です。
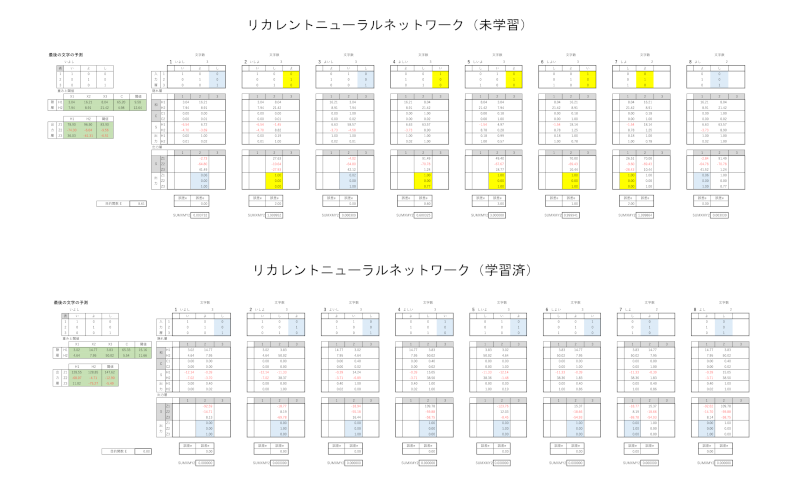
すみませんが、画像は前回同様細かくて数値が読みづらいですが、感覚でお伝えします。
上記の未学習時には、重みと閾値の初期値を設定し、関係式をセルに埋め込んだ状態での表示をしています。
黄色のセルの値は予測した文字と検知した文字とが一致していません。ソルバーを実行することによって目的関数Eが最小値の0になって予測と検知が一致し、青色のセルになっています。
平方誤差eの式はカテゴリデータ(ラベルや文字など)を機械学習で使えるように数値データに変換するOne-hot エンコーディングと呼ばれる方法で(t1,t2,t3)にて表記しています。例えば「い」は(1,0,0)です。
平方誤差e = (t1 – z1)^2 + (t2 – z2)^2 + (t3 – z3)^2
の式はエクセルでSUMXMY2という便利な関数があるので、上記の式の値の下に検証用として求めた値も並記してあります。
ここまでで、リカレントニューラルネットワーク(RNN)のしくみがぼんやりと理解できたような気がしました。エクセルのソルバー実行によって、課題でのAIの「学習」を体感できました。現実的に時系列データの分析に大きな力を発揮しているとの著者の解説に、達成感を感じました。
自己成長やモチベーションの向上にはつながったのではないでしょうか。
でも、まだもやもやしたものがあります。
ニューラルネットワークの「学習」を支える計算法のしくみはよくわかりませんでした。また、エクセルのソルバー実行ということで最適化の計算方法はブラックボックスの中です。
次回(その5)でこの著書『高校数学でわかるディープラーニングのしくみ』の締めくくりとして、ニューラルネットワークの「学習」で最も有名な技法(誤差逆伝播法)のことにも触れて行きたいと思います。
追伸:
この度、“68歳の夢ブログ”の中で会社をつくるための資金稼ぎに、副業としてアフィリエイトを始めました!
ジャンルとしては「学び」とか「転職」で、「シニアの夢」のようなジャンルはASPには無さそうですが、自分が良いと思ったものをしっかり紹介していきたいと思っています。
初心者ですが、勉強しながらコツコツやっていきますので応援よろしくお願いします!



コメント